The Clock Paradox

[Quoted from: American Journal of Physics Vol 31, page 59, 1963. It was adapted by E. F. Taylor and J. A. Wheeler for their book "Space-time Physics".]

In the many discussions of the well-known "clock paradox" of special relativity something of importance has been consistently ignored, namely the time interval DF (Fig. 1).

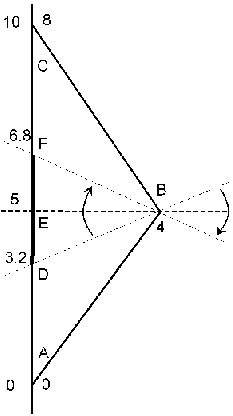
    Fig. 1. Space-time diagram of a rocket flying 
            away from, and returning to, the earth. 

Suppose that a rocket leaves the earth (event A) at 3/5 of the speed of light, flies to a distance of 3 light years, turns abruptly (event B) and returns to the earth at the same speed. During the flight observers on the earth and the rocket will regard each others' clocks as being slowed by a factor of [1 - (3/5)^2]^(1/2) = 4/5.

At event E, the earth observer (whose clock reads 5 years) will calculate (not observe) that the rocket will have reached a point 3 light years away and that the rocket's clock will read 4 years. Event E and B are simultaneous in the earth observer's reference system. As the rocket observer approaches event B, his clock will read 4 years and he will calculate that the earth's clock currently reads 4/5 as much, or 3.2 years. This is perfectly correct since events D and B are simultaneous in the rocket observer's reference system during the outward journey.

When the rocket accelerates abruptly at B, it moves to a new reference system in which the events D and B are no longer simultaneous. The rocket's current hyperplane of simultaneous points swings around so that points F and B become simultaneous.

During the return journey, The rocket's clock records another 4 years, and from the the rocket observer's point of view, the earth clock records another 3.2 years between F and C. If an observer in the rocket presumes to keep a record of the simultaneous reading of the earth's clock, he must advance it by 3.6 years when he accelerates at B. If the rocket observer fails to account for the interval DF when he changes reference systems, he falsely concludes that the earth clock should read only 6.4 years on return, thus yielding the so-called "clock paradox".

We see that the acceleration of an observer induces a rotation of his coordinate axes and coordinate hyperplanes, resulting in an apparent displacement of the current reading of remote clocks. This is a straightforward space-time analog of the fact that the rotation of an observer's reference system attached to the rotating earth results in an apparent displacement of the position of the sun. It need not seem much more mysterious.

Regardless of how an observer's clock is affected by its acceleration, the observer's record of the current reading of remote clocks is drastically altered by the tilting motion of his hyperplane of simultaneity. The extent of such alterations is readily calculated within the special theory of relativity.

***************************************************************

[End of Quote]
Apologies for the gender specific language. 35 years can make a difference.

One goal in publishing the above was to point out that General Relativity is not needed for the analysis. It is entirely practical to model the acceleration of point particles in the Minkowski space-time of special relativity.

Some writers have suggested that "The question ... cannot be answered in the special theory of relativity ..." (C. Moller 1952). A similar comment was made by R. C. Tolman in his 1934 book. It may go back to a 1918 Einstein paper. To me it is not clear whether such statements are about mathematics or physics or psychology. The lack of a simple diagram appears to have clouded serious discussion of relativity for decades and continues to do so.