Ed Lowry
eslowry@alum.mit.edu
users.rcn.com/eslowry

This is a model of an electromagnetic field in space-time. It can be used to help demystify electromagnetism and special relativity. The central stem is the path of a single charged particle through time (the up direction). The slope and density of the surfaces give an integrated measure of both its electric and magnetic fields at each point in space-time as determined by Maxwell's theory of electromagnetism. For a single charged particle, the relationship between the electric and magnetic components of the field can be pictured directly. The image might express the essence of a fundamental physical theory better than any other image. For more complete discussion see American Journal of Physics, pg871, 1963 and Physical Review pg616, 1960.
To understand the model, imagine a charged particle as a tiny sphere bristling with machine guns, each shooting out a continuous stream of bullets. Each bullet moves outward in a straight line at the speed of light. The number of guns is extremely large and proportional to the charge of the particle.
For a stationary particle the streams will form straight lines pointing outward from the particle. The lines becomes less dense moving away from the particle according to the inverse square law. The streams then represent a static electric field of the particle.
If the particle is accelerated the density and direction of the streams still accurately represent its electric field in the Maxwell theory. Its magnetic field is represented by lateral motion of the streams. In the above space-time picture, the streams sweep out surfaces which represent the integrated electromagnetic field.
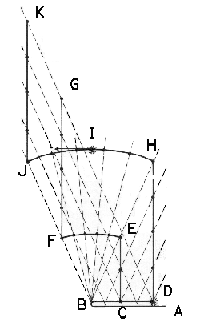
The above picture shows an expanding electromagnetic pulse. A particle moves at fixed speed along a path AB and turns abruptly back along the same path BCD. A machine gun pointing perpendicular to the path will shoot a stream of bullets shown by the kinked line CEFG. A little later the same stream moves to position DHIJK. During the brief acceleration at B bullets are emitted in diverging directions along the dotted lines. An expanding arc of bullets (FE and later JIH) forms an electromagnetic pulse which carries radiant energy moving outward at the speed of light. Where the streams are straight near the particle, they convey no radiant energy.
The lengthening of the arc implies that the density of streams of bullets near it will only decrease in proportion to the distance rather than the square of the distance from B. The density of the bullets has no significance for the field, only the density of the streams. The direction of the arc gives the polarization of the radiation. If the particle is negatively charged, the arc will exert a brief force on a neighboring negative particle at I in a direction opposite to the force which accelerated the first particle at B. An induction coil exploits similar forces to resist the acceleration of electrons in a circuit. A transformer exploits them so that current in one coil induces current in a neighboring coil.
An instantaneous picture of the streams gives the electric field of the charged particle at that instant. The density and direction of the streams in any local region gives the local electric field. If we somehow include in the picture information about the motion of the streams, then we also have full knowledge of the magnetic field of the particle at that instant.
The motion of the streams can be captured by using a space- time picture as shown in the first diagram. The path of the charged particle becomes a mostly vertical stem showing the position of the particle as time progresses. Each stream of bullets sweeps out a surface starting along the stem and radiating outward.
The slope and density of the surfaces then gives a measure of the electromagnetic field of the charged particle at each point in space-time according to the Maxwell theory of electromagnetism. A more complete picture would show a double infinity of surfaces each extending out to infinity.
For purposes of measuring the electromagnetic field, features other than the slope and density of the surfaces may be erased from the picture without losing information about the field. Lines representing the pure electric field or magnetic field or the motion of the bullets or the coordinate planes can all be removed without loss of information about the electromagnetic field. Only the slope and density of the surfaces is needed.
A second charged particle moving through the field experiences a force in the direction of the streams of bullets in its immediate neighborhood. The direction of the streams as seen by a moving particle is given by slicing the field surfaces in such a way that events along the slices are simultaneous in the frame of reference of the second particle. The force is proportional to the charge of the second particle and to the local density of slice lines near it. That force includes the entire effect of the electromagnetic field.

This image shows how the electromagnetic force on an electrically charged particle in a simple case can be interpreted as a magnetic force or as an electric force depending on the frame of reference. At the top, a wire (labelled 1, yellow) is shown with 3 positive charges (labelled 2, red) and 3 negative charges (3, green) in it. The positive charges are stationary and the negative charges are moving along the wire to the left. Each charged particle is shown emitting just one stream of bullets forward (4). A single negative test particle (5, green) is shown near the wire moving to the right.
The current in the wire is said to produce a magnetic field circling the wire and pointing upward near the test particle. The test particle then experiences a magnetic force perpendicular to the field and perpendicular to its own velocity. That force repels the test particle away from the wire. As viewed in the frame of reference of the wire, the wire is electrically neutral so there is no electric force on the test particle, only a magnetic force.
In the lower part of the image a space-time picture shows how these things evolve through time. The wire sweeps out a surface (6, black) at the back. The stationary positive charges sweep out vertical lines (7, red) and the moving negative particles sweep out sloping lines (8, green). The 3 streams of bullets from the positive particle sweep out vertical surfaces (9, red) and the 3 streams from the negative particles sweep out sloping surfaces (10, green). The moving test particle sweeps a sloping line (11, green). The test particle experiences electric forces attracting it toward the positive charges in the wire and repelling it from the negative charges. If the test particle were stationary, those forces would be equal and opposite with a net force on it of zero.
The way the test particle "sees" the electromagnetic field depends on its instantaneous view of the streams of bullets near it. In this image, the test particle is moving to the right and in special relativity, its instantaneous view is not a horizontal slice of the field in space-time but a sloping slice as shown by the plane (12, black) in the foreground. That plane cuts the field surfaces in red and green lines as shown and the green lines are closer together than the red lines implying that the repulsive force is more intense than the attractive force.
In the frame of reference in which the test particle is at rest, it experiences no magnetic force because its velocity is zero, but it does experience a net electric force repelling it away from the wire. The same repulsive force on the test particle is purely magnetic when viewed in the frame of reference of the wire and purely electric when viewed in its own frame of reference. Another way to describe the field would be to say that an electric field is neutralized (by being equal and opposite) when seen by a stationary test particle but is slightly exposed when seen by a moving particle.
With some limitations, the magnetic field at a point can be treated as a measure of the lateral motion of electric fields at that point. One limitation is that such a view becomes overly complex when the field is produced by many particles with different motions. It is then simpler to summarize the moving fields using an electric vector and a magnetic vector at the point. Another limitation is that real charged particles do have a small magnetic moment and in addition there is the theoretical possibility that particles with pure magnetic charge might yet be discovered.
With similar limitations, it is possible to analyze the electromagnetic forces on electrically charged particles without separately considering magnetic fields at all. The magnetic force on an electrically charged particle is always zero in its own frame of reference where its velocity is zero. It would be possible to compute the electric forces on particles and their resulting accelerations in their own frames of reference. The accelerations could then be transformed to a common frame of reference to compute the motion of the particles. While such an approach is not very practical in realistic engineering problems, the possibility of doing so can help give a conceptual feeling for Maxwell's theory applied to particles.
The magnetic field model pictured above exaggerates the difference between the intensity of the attractive and repulsive forces. Electrons move through a wire at a few meters per second which is far less than the speed of light. The ratio of attractive to repulsive forces would differ from 1 by only about 10^-17. However, the pure electrostatic force is huge. We do not experience its full strength because it is normally almost completely neutralized by the close intermixture of positive and negative charges. A small relativistic effect caused by slowly moving electrons in a wire creates a slight imbalance between huge attractive and repulsive forces leading to forces on the order of ounces between wires carrying currents. It could be said that the magnetic forces illustrated are a small but substantial relativistic correction to the much greater electric forces involved.
The above description could be given initially without reference to relativity. The plane of simultaneous events could be referred to as a "conjugate plane" geometrically related to the world line of the particle. After the particle interactions are described in such non-relativistic terms, relativistic ideas could be introduced. That approach to learning relativity can be helpful since:
It seems unlikely that any popular presentation of classical electromagnetism has ever come near the level of clarity which is possible. Popular descriptions by Carl Sagan ("The Demon Haunted World") and Isaac Asimov ("Asimov's new guide to science") describe the electromagnetic field in needlessly complex ways. Carl Sagan even discouraged people from trying to get a common sense understanding of Maxwell's theory saying "In this case common sense is a faithless guide...".
Sagan's view is preceded by a widely used style of describing electromagnetic waves, saying "The changing electric field generates a magnetic field; the changing magnetic field generates an electric field". The fields are correlated that way by Maxwell's equations, but the word "generates" implies a cause- effect relationship which is needlessly indirect and can be misleading. All components of the field are more simply described as generated by the moving charges which provided the source of the waves. As with the pulse described above, the field with all its components simply moves outward from the source and does not change otherwise. With better illustration, common sense can be a very helpful guide.
Moving a magnet near a conductor is said to induce an electric field in the conductor. It would also be appropriate to say that the motion of the magnet exposes an electric field which is neutralized when the magnet is motionless and its opposing electric fields cancel.
The first image above of the Maxwell field was found as a result of efforts to understand physics by translating it into a computer-like language. The clarifying power of the method has encouraged continuing research in the improvement of formal language.
A mathematical description of the field given by this image
is provided in the above journal articles. There too, the
description is simpler than is usually provided. For a particle
with charge e, any event along the world line will have a
velocity given by a 4-vector ui and an
acceleration given by a 4-vector ai. A bullet
emitted at that event will travel at light speed along a null
vector ci to a second event where we can
calculate the field which results from the particle and its
motion at the emission event. The 3 electric and 3 magnetic
components of the field at that event will be given by:
c i × [
u j + ( u j ×
a k ) c k ]
f ij = — — —
—
— — — — — — — —
— — e
4 π ( u m c m )
³
The 2 vectors which combine in the outer cross product are tangent to the surface at the second event, thus specifying its orientation. The field is the sum of two parts, a near field and a far field or radiation component. The near field decreases inversely with the square of the distance from the emission event. The distance is given by vector components of ci. The radiation component is proportional to the acceleration. It dominates at large distances, decreasing only inversely as the distance. This formula is one of the most fundamental in classical physics, but has rarely been used, and almost never presented in this concise form.