My command line program and source code can be downloaded here.

My command line executable can be downloaded here.

A version which prints out the board positions for each solution is here.  Note that printing out the board positions slows down the program quite a bit, so you may want to pipe the output to a text file (nqprint 16 > output.txt) & then examine the results after the program has been run.
 
 

How many ways are there to arrange N non-attacking queens on an N x N chessboard?

For a regular-sized board (8 x 8), there are 92 distinct solutions, one of which is shown above.

Note that for each solution, no two queens can occupy the same column, row or diagonal.

For a 1 x 1 board, there is one trivial solution:
 

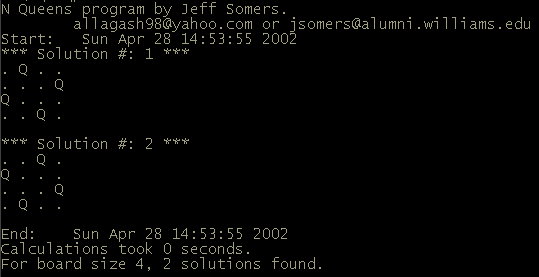
For 2 x 2 and 3 x 3 boards, there are no solutions.  For a 4 x 4 board, there are two:
 
 

These are considered distinct solutions, even though the solutions are mirror images of each other.

My program

There is no quick and easy way to calculate the total number of N queen solutions for an N x N board.

The number of solutions is only known up to board sizes of 23 x 23.

My program is a heavily-optimized C program, yet it still takes over a week for an 800 MHz PC to calculate the number of solutions for a 21 x 21 board.  (In case you're curious, there are 314,666,222,712 solutions.)

2x - 10x speedup over other solutions

My program is almost twice as fast as the program used to calculate the "world record" N queens solution (the 23 x 23 board).  Source for that program, written by Sylvain Pion and Joel-Yann Fourre, can be found here.

It's also up to 10 times as fast the N-queens program written by Dr. Timothy Rolfe. Dr. Rolfe is a computer science professor who has written Algorithm Alley columns for Dr. Dobb's Journal.  His paper on Queens on a Chessboard: Making the Best of a Bad Situation can be found here.
 

To compile the "world record" program in Visual C++, just add algo.c and apart.c to your project.  The board size is hard-coded in algo.h.

To compile Dr. Rolfe's program in Visual C++, just add seq.c to your project.  Then open timers.c and replace the line:

#if defined(__TURBOC__)

with

#if defined(WIN32)

History and Algorithm

The 8 queens problem was studied by Gauss in the mid-1800's.  It is often described in many undergraduate programming texts, since solving it requires students to understand how to program a backtracking algorithm.

The backtracking algorithm used to solve this problem
We place a queen in the top row, then note the column and diagonals it occupies.  We then place a queen in the next row down, taking care not to place it in the same column or diagonal.  We then keep track of the occupied columns and diagonals and move on to the next row.  If no position is open in the next row, we back track to the previous row and move the queen over to the next available spot in its row and the process starts over again.

I became interested in this problem when I was considering taking an Artificial Intelligence course which used LISP as its programming language.  I downloaded a LISP compiler and a sample program which found one solution for the 8 queens problem.  This program was s....l....o....w.  I figured I could write a program in C which found all solutions to the 8 queens problem faster than this LISP program could find one solution.  I was right.  Inspired by the writings of Michael Abrash, I've been trying to optimize that program ever since.

Postscript:  To be fair, the LISP program was not compiled, and since then I've taken that A.I. course and learned to appreciate LISP's strengths.

Further ideas

• I tried caching partial results in order to speed up the program.  A great idea, however it just made things slower.
• Assume we know the results for an N x N board.  Can we somehow leverage that to find the results for an (N + 1) x (N + 1) board?  There doesn't seem to be a away to apply the results of a previous search to the next-greater-board-size search.
• Consider the N Rooks problem.  There's no need to write a program to figure out the solutions, since the number of solutions for a N x N board is n!.  Is there a similar formula for the N Queens problem?

For More Information

Home page of Sylvain Pion, who co-wrote the "world record" N queens code:
http://www-sop.inria.fr/prisme/personnel/pion/index_eng

Home page of Timothy Rolfe, Ph.D.:
http://penguin.ewu.edu/~trolfe/

Eric Weisstein's World of Mathematics:
http://mathworld.wolfram.com/QueensProblem.html

Information on the n Queens problem:
http://www.schoolnet.ca/vp-pv/amof/e_queeI.htm

Interesting chess problem page which appears to be in Czech:
http://web.iol.cz/vaclav.kotesovec/math.htm
 

return to my programming demos page.

You are visitor number