Wittgenstein:
(Emphasis in bold is inserted by Shawver to enhance commentary.) |
Shawver commentary: This section is
concerned with rules and precision of rules and suggests that precision
is not always better than imprecision. |
81. F. P. Ramsey once emphasized
in conversation with me that logic was a 'normative science'. I do not
know exactly what he had in mind, but it was doubtless closely related
to what only dawned on me later: namely, that in philosophy we often compare
the use of words with games and calculi which have fixed rules, but cannot
say that someone who is using language must be playing such a game. --But
if you say that our languages only approximate to such calculi you are
standing on the very brink of a misunderstanding. For then it
may look as if what we were talking about were an ideal language. As if
our logic were, so to speak, a logic for a vacuum. --Whereas logic does
not treat of language -- or of thought -- in the sense in which a natural
science treats of a natural phenomenon, and the most that can be said is
that we construct ideal languages. But here the word "ideal" is liable
to mislead, for it sounds as if these languages were better, more perfect,
than our everyday language; and as if it took the logician to shew people
at last what a proper sentence looked like.
|
81. This is an important aphorism. Early
Wittgenstein, the Wittgenstein of the Tractatus, thought of language as
something like a calculus. The
idea was that if you knew the rules of language, you could apply the calculus
to understand it.
For example, suppose you had the following four sentences:
A. Mary went to the store
B Jack went to the barber.
C Mary is tired
D Jack earns lots of money
And suppose you also had four ways of connecting those sentences:
v - meaning either or both
* - meaning "and"
> - meaning if -then
# - meaning if and only if
And suppose you could also modify any sentence by negating it and symbolizing
that negation with a tilde like this:
~
And let's enrich this calculus. You can also use parentheses.
Using the character names above to name the four sentences, couldn't you
figure out the following statement like one would figure out a calculus?
(A*B) * ~A
It would mean
| While it is true that "Mary went to the store and Jack went to the
Barber" is a true statement it is not true that Mary went to the store. |
And, as you can see, this would not be possible because it is not true
for Mary to have both gone to the store and not to have gone to the store.
So, we can see that the symbolic phrase
(A*B) * ~A
is nonsense. because to be true it would requires A to be both
true and false.
Now, consider the following:
[~(A*B) v (B>C)] v (D#B)
Could this statement be true?
You could figure this out using the same process that we used above
and it would feel very much like performing a kind of mathematical calculus.
This was the sort of vision of language that inspired early Wittgenstein
(and the logical positivists), but now he is saying that it will not work.
One might want to say that if it were a misunderstanding that language
worked as a calculus, then it was because language is defective in some
way. But Wittgensein is telling us that the failure of langauge to
conform to a calculus does not imply that it is defective.
|
| All this, however, can only appear in the right light when one has
attained greater clarity about the concepts of understanding, meaning,
and thinking. For it will then also become clear what can lead us (and
did lead me) to think that if anyone utters a sentence and means or understands
it he is operating a calculus according to definite rules. |
And these concepts of understanding, meaning and
thinking are concepts Wittgenstein will explicate.
|
82. What do I call 'the rule by
which he proceeds'? --The hypothesis that satisfactorily describes
his use of words, which we observe; or the rule which he looks up when
he uses signs; or the one which he gives us in reply if we ask him what
his rule is? --But what if observation does not enable us to see any clear
rule, and the question brings none to light? --For he did indeed give me
a definition when I asked him what he understood by "N", but he was prepared
to withdraw and alter it.-So how am I to determine the rule according to
which he is playing? He does not know it himself. --Or, to ask a better
question: What meaning is the expression "the rule by which he proceeds"
supposed to have left to it here?
|
82. Suppose you are playing chess and you move your
knight. A child who does know how to play chess asks you how you
were able to move the piece in such an odd way. If you know chess,
the rule is probably clear in your mind and you can state it unambiguously.
You can say what the rule is that guides and constrains the movement of
the bishop, compared to the movement of the knight. There is no ambiguity
here.
But if you were asked the rule you used to decide if a sentence were
a well formed sentence, or grammatically flawed, you might find that you
do not know the answer immediately. You feel you have to think about
it a bit. It may be that you can choose which sentence has a flaw,
but not know immediately what the rule that this correct useage obeys.
Similarly, you might know how to use a word in a sentence, and use it
regularly and meaningfully, yet still not be know its useage well enough
to give a definition spontaneously and easily.
So, ask yourself, are you following a rule in the cases in which you
cannot easily and spontaneously state the rule? In what sense are
you following one? Are you subsequently just trying to discover a
stated rule that wold capture the behavior you are engaging in without
any sense of trying to conform to a defined rule? |
| 83. Doesn't the analogy between
language and games throw light here? We can easily imagine people amusing
themselves in a field by playing with a ball so as to start various existing
games, but playing many without finishing them and in between throwing
the ball aimlessly into the air, chasing one another with the ball and
bombarding one another for a joke and so on. And now someone says: The
whole time they are playing a ball-game and following definite rules at
every throw. |
83. See how far this new model of language
is from the model of language as a calculus? Yes, there are rules,
but the rules are not binding in the same way that they are in calculus.
The rules of langauge do not confine every movement that is made.
In languge, one can stop, metaphorically speaking, to toss the ball up
into the air.
|
And is there not also the case where we play and-make up the rules
as we go along? And there is even one where we alter them-as we go along.
|
This is a particularly significant observation.
In language we will find ourselves making up meanings for words as we go
along. "What do you mean by that?" someone asks you. Then you
say, "I mean..." and you give the word a definite sense, not a sense that
is quite what it is in the dictionary, but a definite sense. You
are making up the rules of this language game as you go along. |
84. I said that the application of a word
is not everywhere bounded by rules. But what does a game look like that
is everywhere bounded by rules? whose rules never let a doubt creep in,
but stop up all the cracks where it might? -- Can't we imagine a rule determining
the application of a rule,
and a doubt which it removes-and so on? |
84. Am I right that games are not completely bounded
by rules? Sure, there are gaps in the stated rules. But can't we
imagine some sort of implicit rule that guides us in the spaces between
the rules?
|
| But that is not to say that we are in doubt because
it is possible for us to imagine a doubt. I can easily imagine someone
always doubting before he opened his front door whether an abyss did not
yawn behind it, and making sure about it before he went through the door
(and he might on some occasion prove to be right)-but that does not make
me doubt in the same case. |
Sure, we can imagine such a thing, but we need not.
It is not a requirement of games that they be everywhere bounded by rules.
|
85. A rule stands there like a sign-post.--Does
the sign-post leave no doubt open about the way I have to go? Does it shew
which direction I am to take when I have passed it; whether along the road
or the footpath or cross-country? But where is it said which way I am to
follow it; whether in the direction of its finger or (e.g.) in the opposite
one? --And if there were, not a single sign-post, but a chain of
adjacent ones or of chalk mar
ks on the ground-- is there only one way of interpreting them?-- So
I can say, the sign-post does after all leave no room for doubt. Or rather:
it sometimes leaves room for doubt and sometimes not. And now this is no
longer a philosophical proposition,
but an empirical one. |
85. And even if we stated rules (like sign-posts)
every space, this would not leave us with some flexibility in how we played
the game. Even sign-posts have to be interpreted. Even if a
hand
points in a certain direction, where is the rule that says I must follow
it in the direction of the finger?
And even if we assume that the hand points towards the flag, is it pointing
to the stripes or the stars? Or the flag as a whole? Or to
the colors? Is there not room for interpretation here? Is everything
completely bound by rules? And if we have this flexibility in pointing,
is there not room for a similar flexibility in how we interpret the rules
of a game?
|
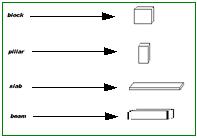
86. Imagine a language-game like (2)
played with the help of a table. The signs given to B by A are now written
ones. B has a table, in the first column are the signs used in the game,
in the second pictures of building stones. A shews B such a written sign;
B looks it up in the table, looks at the picture opposite, and so on. So
the table is a rule which he follows in executing orders.-One learns to
look the picture up in the table by receiving a training, and part of this
training consists perhaps in ~e pupil's learning to pass with his finger
horizontally from left to right; and so, as it were, to draw a series of
horizontal lines on the table. |
Imagine the workers in a language-game like
(2)
having the following table to use to make their selection of stones.
|
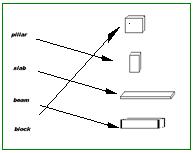
Suppose different ways of reading a table were now
introduced; one time, as above, according
to the schema:
|
If we did include arrows in our own culture, it would
likely look like this:
For the most part, however, the action that the arrows prompt is so common
in our own culture that the arrows are not needed. We all approach
such tables with our eyes already trained to look in the way the arrows
are intended to guide us. |
another time like this:
or in some other way.
|
For this kind of looking, however, we would need
arrows:
|
| --Such a schema is supplied with the table as the rule for its use. |
But what Wittgensein had in mind for this tribe is
two tables. For exxample, imagine one being up on a wall, and the
other being in one's hand.
|
|
However, if their mythology required a more complex, the rule might
be:
|
|
Or, imagine things more complex,, still. Perhaps
this language game is not for the purpose of building but for the purpose
of assuaging the temper of the gods, and supppose, too, that the paths
the gods want their servants to take to read these tables requires them
to work through a maze of arrows such as this:
in order to read a table like this:
|
| Can we not now imagine further rules to explain this one? |
Now, suppose the various rules in the network of
arrows was tied to a mythology so that each arrow represented a sacred
path that must be followed exactly. Not only did this sacred path
guide how one's eyes were to move, but also how one stood and the expression
one put on one's face:
|
| And, on the other hand, was that first table incomplete without the
schema of arrows? And are other tables incomplete without their schemata? |
The initial table seemed easy to us:
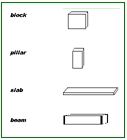 |
But the ease we felt surely reflected the years of training we had
in reading such a table. We no longer needed guidance to look from
left to right. The straight arrows may have provided |
such guidance to one uninitiated, but only if that person had already had
training in how to read arrows, how to follow a line with the eyes.
Years of reading make it natural for English speaking people to follow
the line from left to right, but, of course, there are other traditions.
We could complicate things further by a requirement that the reader of
the table must jump from line to line, or move the eyes back and forth,
or up and down the line. There is no end of complicating possibilities.
Yet, these possibilities do not confuse us. We have been trained
to see and read such tables so we do with ease, just as we have been trained
to read the words on this page and do that with ease -- even though it
was not always so.
All these implicit rules seem to guide our behavor, and rules we can
no longer state, that no longer guide us in a concscious way. Do
we want to say that the table needed to include such rules in order to
be complete? If so, would any table ever be complete?
|
87. Suppose I give this explanation:
| I take 'Moses' to mean the I man, if there was such a man, who led
the Israelites out of Egypt, whatever he was called then and whatever he
may or may not have done besides." -- |
|
87. LW is going to try to show us (or remind
us) how difficult it can be to tie down the meaning of even an apparently
simple sentence. This may seem to you like a change in subject, because
we are no longer talking about tables and arrows, but the subject is much
the same. We are noticing how many gaps there are in the rules we
might use to interpret things, how much of our understanding takes place
without our noticing how it all works. |
| But similar doubts to those about "Moses" are
possible about the words of this explanation (what are you calling "Egypt",
whom the "Israelites" etc.?). Nor would these questions come to an end
when we got down to words like "red", "dark", "sweet". |
As soon as you try to pin down these words, you can
see how hard it is to make sure the person in history that we talk about
refers to "Moses." Maybe the real person had a different name and maybe
his story has been modified through the years. Has it been so modified
that the person we think of as "Moses" is no longer congruent with the
historical figure? It is possible to doubt all of these things. |
| "But then how does an explanation help me to understand, if after
all it is not the final one? In that case the explanation is never completed;
so I still don't understand what he means, and never shall!" --
As though an explanation as it were hung in the air unless supported
by another one. |
This is Wittgenstein's questioning voice, voice of
aporia,
wondering. If I can't tie these things down with an explanation,
I not only fail to understand who Moses is, but I fail in all similar attempts.
Exaplanations cannot help me understand! (or so it seems to the aporetic
voice).
It seems (when in this apoetic mood) that we must be able
to use explanations to tie down all the ambiguities, or else nothing will
ever be known.
|
| Whereas an explanation may indeed rest on another one that has been
given, but none stands in need of another -- -unless we require it to prevent
a misunderstanding. |
That is, we may be able to use one explanation to
explain another -- but no additional explanation is needed except
to prevent misunderstanding. You do not need an explanation for the
statement "The chair I am sitting in is uncomfortable," unless you don't
understand it (and you might not, for example, if it looked o you that
I was not sitting at all.) |
| One might say: an explanation serves to remove or to avert a misunderstanding
-- one, that is, that would occur but for the explanation not every one
that I can imagine. |
The confusion comes about because we imagine that
explanations contain a complete rule that require no training to interpret.
Explanations canavert misunderstandings but only for those whose training
is sufficient to understand the explanation. And, we cannot find
sufficient explnations to replace that history of training. |
It may easily look as if every doubt merely revealed an existing gap
in the foundations; so that secure understanding is only possible
if we first doubt everything that can be doubted, and then remove all
these doubts.
|
This is reminescent of Decartes' "Cartesian doubt",
or "methodological doubt." His idea was, you'll recall, that he could
doubt everything except that he was thinking (I think, therefore I am).
Everything that came after that point in the Cartesian text was the result
of his reasoning things out, and thus proven, ostensibly, by the reasoning.
It looks as though we must pin things down completely. We must find
a way to prove, for example, that historical person I call Moses is indeed
he "real Moses" or else it is all a sham. But how many stories about
Moses would have to be a little wrong, in order to call it all a sham?
And even if the stories were quite a bit wrong, would it be a sham?
What does it mean, in fact, for any name to refer to an historical figure
with accuracy? It seems it does not make sense if we cannot pin things
like this down. On the other hand, the assertions do make some kind
of sense to us, given our training in this story of Moses -- even though
we cannot pin things like this down without becoming aware of the enormity
of doubt about all the details. |
The sign-post is in order -- if, under normal circumstances, it fulfills
its purpose.
|
When does the explanation, the reasoning come to
an end? Remember, we may not need an explanation at all. If we are
already trained or practiced in how to interpret some sign, then the explanation
is no longer required. If there is a stop sign, or some strange sign,
it needs no explanation if we have been trained in its interpretation.
Consider the explanation I gave those reading over our shoulder at the
top of this note. I explained our tradition that we put our initials in
brackets around the text. But I did not explain that Judy uses small
characters for her initials, or that Nick sometimes uses no brackets at
all. Will they understand? Is it possible that they will simply
make sense of it even if I don't explain these details? At what point will
the explanation be more than is necessary? |
| 88. If I tell someone "Stand
roughly here"-- may not this explanation work perfectly? And cannot every
other one fail too? |
88. If I want to take a photograph of someone, I
might say, "stand roughly here". That means, I am likely to
be satisfied if the person stands somewhere withina range of places.
Of course, the person might stand outside my preferred range, or I might
discover that the range of places I thought would work will not work. On
the other hand, I cannot guard against this kind of problem entirely by
being more specific. Imagine my saying, "Stand on this blade
of grass." Couldn't I find this positioning not quite satisfactory,
too? |
| But isn't it an inexact explanation? - |
This is really the voice of Ramsey again, or perhaps
the voice of early Wittgenstein or one of the positivists who tried to
reduce language to a kind of calculus.
This
voice has been very influential in the development of modern psychology.
This voice says, "Can't we find a way to represent our thoughts and wishes
very precisely so that there can be no misunderstanding? The usefulness
of phrases such as "stand roughly here" helps disenchant us with this quest
by showing us |
| Yes; why shouldn't we call it "inexact"? Only let us understand what
"inexact" means. For it does not mean "unusable". |
that non-exact explanation can be very useful, indeed. |
| And let us consider what we call an "exact" explanation in contrast
with this one. Perhaps something like drawing a chalk line round an area?
Here it strikes us at once that the line has breadth. So a colour-edge
would be more exact. But has this exactness still got a function here:
isn't the engine idling? |
In this paragraph, Wittgenstein argues that not only
is non-precise language often useful, but that more precise statements
(e.g., stand precisely on this blade of grass) adds nothing to the usefulness,
at times, of less precise statements. You could stand on a precise
blade of grass if I stand "stand roughly over there" but it wouldn't be
more useful than if you stood in a slightly different place. This
is what Wittgenstein has in mind when he suggests that this exactness does
not have a function in some contexts. |
| And remember too that we have not yet defined what is to count as overstepping
this exact boundary; how, with what instruments, it is to be established.
And so on. |
Even when we try to be more precise (you must step
on this precise blade of grass) we do not elminate all imprecision.
Even here, we must define what will count as not doing what the precise
rule
calls on us to do. |
| We understand what it means to set a pocket watch
to the exact time or to regulate it to be exact. But what if it were asked:
is this exactness ideal Of course, we can speak of measurements of time
in which there is a different and as we should say a greater, exactness
than in the measurement of time by a pocket-watch; in which the words "to
set the clock to the exact time" have a different, though related meaning,
and 'to tell the time' is a different process and so on.-- |
Even when we talk about precision, it is not
clear how precise precision must be in order to be precise enough. |
| Now, if I tell someone: "You should come to dinner more punctually;
you know it begins at one o'clock exactly"-- |
Here's another example to examine, to help us understand
the function and limits of our ideal of precision. How precise would such
a statement be? |
| is there really no question of exactness here? because it is possible
to say: "Think of the determination of time in the laboratory or the observatory;
there you see what 'exactness' means"? exactness, or how nearly does it
approach the ideal?- |
The first thing to notice is that the kind of "exactness"
that would be required for someone coming to dinner punctually is not of
the same level as that is required in a laboratory or an observatory.
The context lets us know that different levels of precision are involved
in these different situations. |
| "Inexact" is really a reproach, and "exact" is praise.
And that is to say that what is inexact attains its goal less perfectly
than what is more exact. Thus the point here is what we call "the goal".
Am I inexact when I do not give our distance from the sun to the nearest
foot, or tell a joiner the width of a table to the nearest thousandth of
an inch? |
Language is often implicitly loaded to convince us
that something is good or bad. People who call someone "youthful"
for example are using loaded langauge to communicate a positive quality
about behavior or appearance that xome might refer to more negatively as
"childish". Sometimes, it is hard to find the negative loading for
a positive term (or the positive loading for a negative term) and our languuge
simply doesn't appear to have the resources for thinking about the object
without this particular evaluative loading.
That may be the case for the notion of "exactness" has that kind of
positive loading. (see my comments on "transvaluation") |
| No single ideal of exactness has been laid down;
we do not know what we should be supposed to imagine under this head
-- unless you yourself lay down what is to be so called. But you will kind
it difficult to hit upon such a convention; at least any that satisfies
you. |
What all of this study of exactness seems
to be teling us is that how much "exactness" we need depends upon the context.
Sometimes demands for "exactness" can just be a bother with nothing useful
to add. Because they would be a "bother", this excessive precision
is not so universally ideal as our language suggests to us. |