Foundations of Modern Cosmology

{Credit University of Virginia, Department of Astronomy}

{Aside Comment: Black hole limits are related to hysteresis analysis limitations.}

Chapter 9: Black Holes

Chapter Summary Almost as soon as the Einstein equations were published, Karl Schwarzschild found the first exact solution. The Schwarzschild metric is our first example of a full general relativistic spacetime; it describes the vacuum exterior to a sphere of mass M. The metric coefficients provide the mathematical description of gravitational time dilation and length contraction outside the sphere. The effects are strongest near the Schwarzschild radius, Rs = 2GM/c2. A black hole is an object whose mass lies entirely within its Schwarzschild radius. The event horizon is the point of no return around a black hole. Once inside the event horizon, which for a nonrotating hole lies at the Schwarzschild radius, nothing, not even light, can escape. At the Schwarzschild radius the gravitational time dilation goes to infinity and lengths are contracted to zero. An observer at infinity watching a probe approach a black hole would see the probe's signals redshifted further and further, till at last the redshift would approach infinity and no more photons escaped, but the distant observer would never see the probe cross the event horizon. To a sufficiently small probe, however, nothing unusual would occur at the horizon. (A large probe and/or a small hole would result in tidal forces tearing the probe apart.) But once across the horizon, the probe is doomed to fall into the singularity at the center.

The last stable orbit at 3Rs is the closest at which a material particle can orbit the hole; any closer in and the particle must move radially inward or outward. The photon sphere is the radius 1.5Rs at which gravity bends the path of photons so much that light orbits the hole circularly.

A Kerr hole is a spinning black hole. The single event horizon of a Schwarzschild black hole splits into an outer static surface and an inner ellipsoidal event horizon. Between the two surfaces is the ergosphere. At the static surface, it is necessary to move at the speed of light opposite the rotation of the hole just in order to stay still; further inward even light is dragged around with the hole. The no-hair theorem states that a static black hole is completely described by three quantities: mass, angular momentum, and charge, though a black hole would be unlikely to retain any electrical charge for long in the real universe.

Hawking radiation is the emission of particles (mostly photons) by black holes. Hawking radiation is blackbody and permits a temperature to be assigned to a black hole. The temperature leads to a thermodynamics of black hole and a definition of their entropy; black holes are found to have the highest entropy of any object in the universe. However, Hawking radiation is miniscule for all black holes of any significant size. Hawking radiation is a quantum effect, but exotic properties also come from classical (i.e. non-quantum) black holes. The throats of black holes could create wormholes, which might join two distant regions of spacetime. Wormholes also can have closed timelike paths associated with them, although it is unlikely that anything larger than a subatomic particle could traverse them. However, wormholes are dynamic and pinch off, making them useless for transportation, since anything in the wormhole would be crushed at the singularity. Another strange solution is the "white hole," which in many respects is the mirror image of the black hole; rather than matter disappearing into the hole, matter appears at a white hole, and nothing can remain in the white hole. However, there is no evidence that white holes could form in the physical universe. Black holes are created when massive stars collapse, or perhaps by the collapse of extremely dense star clusters at the center of galaxies, but white holes would have to be placed ab initio into the universe.

Accretion Disk Fig. 9.8: An accretion disk in a binary system
 

Active Galaxies are galaxies that show energetic activity in their cores. The best model for the "central engine" of active galaxies is a supermassive black hole in the center of the galaxy. Around this hole a huge disk of gas, an accretion disk , slowly spirals into the hole and releases energy. 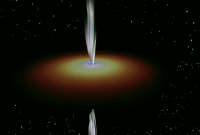Disk and Jet

Artist's conception of an accretion disk and jet in an active galaxy. (Credit: Greg Foss, PSC)
 

The HST has looked deep into the heart of some nearby active galaxies. These galaxies exhibit jets shooting out from their cores at relativistic energies and speeds. One image shows the giant elliptical galaxy, M87, and the other shows the active galaxy NGC4261. A gravitational lens is produced when light passes through the enormous gravitational field of an object, such as a massive galaxy. In this image we see a background object lensed into four faint blue images surrounding a brigher red elliptical galaxy. Lenses such as these provide important cosmological data such as distances to very remote galaxies.

Gravity Lens A gravitational lens found by HST

Another gravitational lens is produced by a cluster of galaxies. The arcs are the distorted images of even more distant galaxies lying behind the cluster.

Points to Ponder
  • What is meant by singularity? What is a coordinate singularity?
  • What novel features do spinning black holes possess? How could an advanced civilization extract energy from a Kerr black hole? Why is this still not an infinite source of energy?
  • When, if ever, is Hawking radiation important?
Potential Pitfalls The Schwarzschild metric applies to the (vacuum) region outside any spherical object, including relatively puny bodies such as the Earth and Sun. For any object that extends beyond its Schwarzschild radius, no event horizon or other strange effects exist. The metric within a normal object is some other metric, appropriate to a matter-filled sphere. Only in the case that an object collapses to beneath its Schwarzschild radius does a black hole form. However, some of the effects of the Schwarzschild metric can be observed even for the weak field of the Earth. Gravitational redshift has been measured for light falling toward the Earth, and a slight frame-dragging effect occurs even for objects such as the Earth and Sun.